4.12. Programación dinámica¶
Muchos programas en ciencias de la computación se escriben para optimizar algún valor; por ejemplo, encontrar el camino más corto entre dos puntos, encontrar la línea que mejor se ajusta a un conjunto de puntos, o encontrar el conjunto más pequeño de objetos que satisface algunos criterios. Hay muchas estrategias que usan los científicos de la computación para resolver estos problemas. Uno de los objetivos de este libro es presentarle a usted varias estrategias de solución de problemas diferentes. La programación dinámica es una estrategia para estos tipos de problemas de optimización.
Un ejemplo clásico de un problema de optimización consiste en dar las vueltas utilizando el menor número de monedas. Supongamos que usted es un programador para un fabricante de máquinas expendedoras. Su empresa desea agilizar el esfuerzo dando la menor cantidad posible de monedas para las vueltas de cada transacción. Supongamos que un cliente inserta un billete de un dólar y compra un ítem de 37 centavos. ¿Cuál es el menor número de monedas que usted puede usar para dar las vueltas? La respuesta es seis monedas: dos de 25 centavos, una de 10 centavos, y tres de un centavo. ¿Cómo llegamos a la respuesta de seis monedas? Comenzamos con la moneda más grande de nuestro arsenal (la de 25 centavos) y usamos la mayor cantidad posible, luego vamos a la siguiente moneda de menor valor y usamos el mayor número posible. Este primer enfoque se llama un método codicioso porque tratamos de resolver una gran parte del problema tan inmediatamente como sea posible.
El método codicioso funciona bien cuando usamos monedas estadounidenses, pero supongamos que su empresa decide instalar sus máquinas expendedoras en Elbonia donde, además de las monedas usuales de 1, 5, 10 y 25 centavos, también tienen una moneda de 21 centavos. En este caso, nuestro método codicioso no logra encontrar la solución óptima para las vueltas de 63 centavos. Con la adición de la moneda de 21 centavos, el método codicioso aún hallaría que la solución es de seis monedas. Sin embargo, la respuesta óptima es tres monedas de 21 centavos.
Veamos un método con el que podríamos estar seguros de que encontraríamos la respuesta óptima al problema. Dado que esta sección trata sobre la recursividad, usted quizás ya habrá adivinado que usaremos una solución recursiva. Comencemos con la identificación del caso base. Si estamos tratando de dar unas vueltas que corresponden a la misma cantidad que el valor de una de nuestras monedas, la respuesta es fácil, una moneda.
Tenemos varias opciones si la cantidad no coincide. Lo que queremos es el mínimo valor resultante entre las siguientes opciones: a) un centavo más el número de monedas necesarias para dar las vueltas por la cantidad original menos un centavo, o b) una moneda de 5 centavos más el número de monedas necesarias para dar las vueltas por la cantidad original menos cinco centavos, o c) una moneda de 10 centavos más el número de monedas necesarias para dar las vueltas por la cantidad original menos diez centavos, y así sucesivamente. Por lo tanto, el número de monedas necesarias para dar las vueltas por la cantidad original se puede calcular de acuerdo con la siguiente expresión:
El algoritmo para hacer lo que acabamos de describir se muestra en el Programa 7. En la línea 3 estamos verificando nuestro caso base; es decir, estamos tratando de dar las vueltas correspondientes a la cantidad exacta de una de nuestras monedas. Si no tenemos una moneda igual a la cantidad de las vueltas, hacemos llamadas recursivas para cada valor de moneda diferente menor que la cantidad de las vueltas que estamos tratando de generar. La línea 6 muestra cómo filtramos la lista de monedas a aquéllas que sean menores que el valor actual de las vueltas usando una comprensión de listas. La llamada recursiva también reduce la cantidad total de las vueltas que necesitamos generar con el valor de la moneda seleccionada. La llamada recursiva se hace en la línea 7. Note que en esa misma línea sumamos 1 a nuestro número de monedas para explicar el hecho de que estamos usando una moneda. Simplemente sumar 1 es lo mismo que si hubiéramos hecho una llamada recursiva en la cual satisfacemos la condición del caso base inmediatamente.
Programa 7
1 2 3 4 5 6 7 8 9 10 11 12 | def vueltasRec(listaValoresMonedas,vueltas):
minMonedas = vueltas
if vueltas in listaValoresMonedas:
return 1
else:
for i in [m for m in listaValoresMonedas if m <= vueltas]:
numeroMonedas = 1 + vueltasRec(listaValoresMonedas,vueltas-i)
if numeroMonedas < minMonedas:
minMonedas = numeroMonedas
return minMonedas
print(vueltasRec([1,5,10,25],63))
|
El problema con el algoritmo del Programa 7 es que es extremadamente ineficiente. De hecho, requiere 67.716.925 llamadas recursivas para encontrar la solución óptima al problema de los 63 centavos usando 4 monedas. Para entender la falla fatal en nuestro enfoque, mire la Figura 3, que ilustra una pequeña fracción de las 377 llamadas de función necesarias para encontrar el conjunto óptimo de monedas para dar unas vueltas de 26 centavos.
Cada nodo en la gráfica corresponde a una llamada a la función vueltasRec. La etiqueta en el nodo indica el valor de las vueltas para el que estamos calculando el número de monedas. La etiqueta de la flecha indica la moneda que acabamos de usar. Siguiendo la gráfica podemos ver la combinación de monedas que nos ha llevado a cualquier punto de la gráfica. El principal problema es que estamos recalculando demasiado. Por ejemplo, la gráfica muestra que el algoritmo recalcularía el número óptimo de monedas para unas vueltas de 15 centavos al menos tres veces. Cada uno de estos cálculos para encontrar el número óptimo de monedas para 15 centavos, en sí mismo, implica 52 llamadas a la función. Es evidente que estamos perdiendo mucho tiempo y esfuerzo recalculando resultados anteriores.
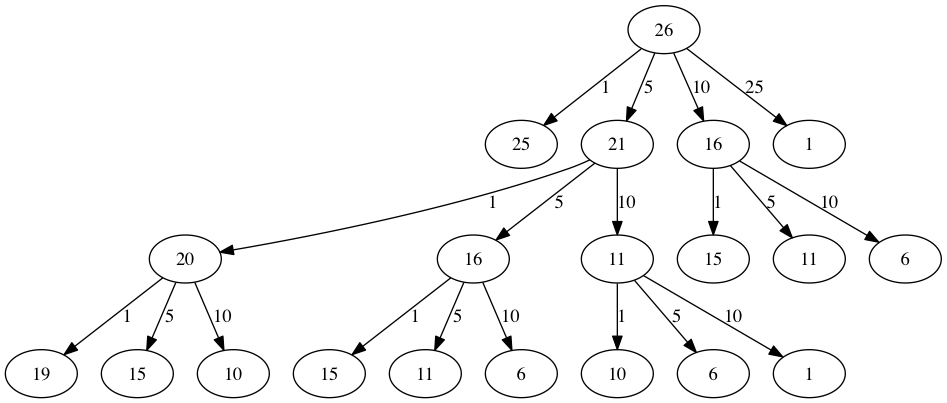
Figura 3: Árbol de llamadas a la función para el Programa 7¶
Figura 3: Árbol de llamadas a la función para el Programa 7
La clave para reducir la cantidad de trabajo que hacemos es recordar algunos de los resultados pasados de modo que podamos evitar recalcular los resultados que ya conocemos. Una solución simple es almacenar los resultados en una tabla para el número mínimo de monedas cuando los encontremos. Entonces antes de calcular un nuevo mínimo, primero buscamos en la tabla para ver si un resultado ya es conocido. Si ya hay un resultado en la tabla, usamos el valor de la tabla en lugar de recalcularlo. El ActiveCode 1 muestra un algoritmo modificado para incorporar nuestro esquema de búsqueda en tabla.
Note que en la línea 6 hemos añadido una verificación para ver si nuestra tabla contiene el número mínimo de monedas para cierta cantidad de vueltas. Si no lo contiene, calculamos dicho mínimo recursivamente y almacenamos el mínimo calculado en la tabla. El uso de este algoritmo modificado reduce a 221 el número de llamadas recursivas que necesitamos hacer para el problema de los 63 centavos usando 4 monedas.
Aunque el algoritmo en el AcitveCode 1 es correcto, se ve y se siente como un poco artificioso. Además, si miramos las listas de resultadosConocidos podemos ver que hay algunos vacíos en la tabla. De hecho, el término para lo que hemos hecho no es programación dinámica, sino que hemos mejorado el rendimiento de nuestro programa mediante el uso de una técnica conocida como “memoización”, o más comúnmente llamado “cacheo”.
Un verdadero algoritmo de programación dinámica adoptará un enfoque más sistemático del problema. Nuestra solución de programación dinámica va a empezar con dar las vueltas por un centavo y sistemáticamente ascenderá hasta la cantidad de vueltas que necesitamos. Esto nos garantiza que en cada paso del algoritmo ya sabemos el número mínimo de monedas necesarias para dar las vueltas correspondientes a cualquier cantidad menor.
Veamos cómo llenaremos una tabla de cantidades mínimas de monedas para usar al dar unas vueltas de 11 centavos. La Figura 4 ilustra el proceso. Empezamos con un centavo. La única solución posible es una moneda (una de un centavo). La fila siguiente muestra la cantidad mínima de monedas para un centavo y para dos centavos. Una vez más, la única solución es dos monedas de un centavo. La quinta fila es donde las cosas se ponen interesantes. Ahora tenemos dos opciones a considerar, cinco monedas de un centavo o una de 5 centavos. ¿Cómo decidimos cuál es el mejor opción? Consultamos la tabla y vemos que el número de monedas necesarias para dar las vueltas por cuatro centavos es cuatro, más un centavo adicional para completar cinco, lo cual da como resultado cinco monedas. O podemos fijarnos en cero centavos más una moneda de 5 centavos para completar cinco centavos, lo cual da como resultado una 1 moneda. Como el mínimo entre uno y cinco es uno, almacenamos 1 en la tabla. Avance rápidamente al final de la tabla y considere el caso de 11 centavos. La Figura 5 muestra las tres opciones que tenemos que considerar:
Una moneda de un centavo más el número mínimo de monedas para dar unas vueltas de \(11-1 = 10\) centavos (1)
Una moneda de 5 centavos más el número mínimo de monedas para dar unas vueltas de \(11 - 5 = 6\) centavos (2)
Una moneda de 10 centavos más el número mínimo de monedas para dar unas vueltas de \(11 - 10 = 1\) centavo (1)
Bien sea la opción 1 o la 3 nos dará un total de dos monedas que es el número mínimo de monedas para completar 11 centavos.
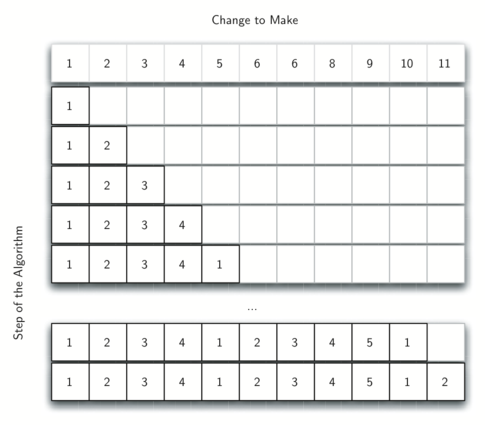
Figura 4: Mínimo número de monedas necesarias para dar las vueltas¶
Figura 4: Mínimo número de monedas necesarias para dar las vueltas
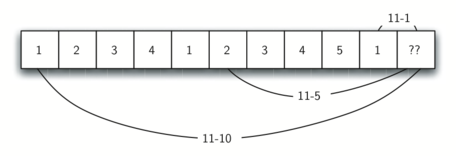
Figura 5: Tres opciones a considerar para el número mínimo de monedas para completar once centavos¶
Figura 5: Tres opciones a considerar para el número mínimo de monedas para completar once centavos
El Programa 8 es un algoritmo de programación dinámica para solucionar nuestro problema de de dar las vueltas. vueltasProgDin tiene tres parámetros: una lista de valores válidos de monedas, la cantidad de vueltas que queremos completar y una lista del número mínimo de monedas necesarias para completar cada valor. Cuando la función termine, minMonedas contendrá la solución para todos los valores desde 0 hasta el valor de vueltas.
Programa 8
def vueltasProgDin(listaValoresMonedas,vueltas,minMonedas):
for centavos in range(vueltas+1):
conteoMonedas = centavos
for j in [m for m in listaValoresMonedas if m <= centavos]:
if minMonedas[centavos-j] + 1 < conteoMonedas:
conteoMonedas = minMonedas[centavos-j]+1
minMonedas[centavos] = conteoMonedas
return minMonedas[vueltas]
Note que vueltasProgDin no es una función recursiva, a pesar que empezamos con una solución recursiva a este problema. Es importante darse cuenta de que sólo porque usted sea capaz de escribir una solución recursiva a un problema no significa que ésa sea la solución mejor o más eficiente. La mayor parte del trabajo en esta función se realiza mediante el ciclo que comienza en la línea 4. En este ciclo consideramos el uso de todas las monedas posibles para dar las vueltas por la cantidad especificada por centavos. Como hicimos con el ejemplo de 11 centavos descrito arriba, recordamos el valor mínimo y lo guardamos en nuestra lista minMonedas.
Aunque nuestro algoritmo de dar las vueltas hace un buen trabajo para averiguar el número mínimo de monedas, no nos ayuda a dar las vueltas, ya que no realiza un seguimiento de las monedas que usamos. Podemos extender la función vueltasProgDin fácilmente para realizar un seguimiento de las monedas usadas recordando simplemente la última moneda que agregamos para cada entrada de la tabla minMonedas. Si conocemos la última moneda añadida, simplemente podemos restar el valor de la moneda para encontrar una entrada anterior en la tabla que nos diga la última moneda que agregamos para completar esa cantidad. Podemos seguir retrocediendo por la tabla hasta que lleguemos al principio.
El ActiveCode 2 muestra el algoritmo vueltasProgDin modificado para realizar un seguimiento de las monedas utilizadas, junto con una función imprimirMonedas que recorre la tabla para imprimir el valor de cada moneda usada. Esto muestra el algoritmo en acción resolviendo el problema para nuestros amigos en Elbonia. Las dos primeras líneas de main fijan la cantidad a convertir y crean la lista de monedas usadas. Las dos líneas siguientes crean las listas que necesitamos para almacenar los resultados. monedasUsadas es una lista de las monedas usadas para dar las vueltas, y conteoMonedas es el número mínimo de monedas usadas para dar las vueltas por la cantidad correspondiente a la posición en la lista.
Note que las monedas que imprimimos vienen directamente del arreglo monedasUsadas. Para la primera llamada comenzamos en la posición 63 del arreglo y se imprime 21. Luego tomamos \(63 - 21 = 42\) y miramos el elemento 42 de la lista. Una vez más encontramos un 21 almacenado allí. Finalmente, el elemento 21 del arreglo también contiene 21, dándonos las tres monedas de 21 centavos.