7.21. Discussion Questions¶
Draw the tree structure resulting from the following set of tree function calls:
>>> r = BinaryTree(3) >>> insertLeft(r,4) [3, [4, [], []], []] >>> insertLeft(r,5) [3, [5, [4, [], []], []], []] >>> insertRight(r,6) [3, [5, [4, [], []], []], [6, [], []]] >>> insertRight(r,7) [3, [5, [4, [], []], []], [7, [], [6, [], []]]] >>> setRootVal(r,9) >>> insertLeft(r,11) [9, [11, [5, [4, [], []], []], []], [7, [], [6, [], []]]]
Trace the algorithm for creating an expression tree for the expression \((4 * 8) / 6 - 3\).
Consider the following list of integers: [1,2,3,4,5,6,7,8,9,10]. Show the binary search tree resulting from inserting the integers in the list.
Consider the following list of integers: [10,9,8,7,6,5,4,3,2,1]. Show the binary search tree resulting from inserting the integers in the list.
Generate a random list of integers. Show the binary heap tree resulting from inserting the integers on the list one at a time.
Using the list from the previous question, show the binary heap tree resulting from using the list as a parameter to the
buildHeapmethod. Show both the tree and list form.Draw the binary search tree that results from inserting the following keys in the order given: 68,88,61,89,94,50,4,76,66, and 82.
Generate a random list of integers. Draw the binary search tree resulting from inserting the integers on the list.
Consider the following list of integers: [1,2,3,4,5,6,7,8,9,10]. Show the binary heap resulting from inserting the integers one at a time.
Consider the following list of integers: [10,9,8,7,6,5,4,3,2,1]. Show the binary heap resulting from inserting the integers one at a time.
Consider the two different techniques we used for implementing traversals of a binary tree. Why must we check before the call to
preorderwhen implementing as a method, whereas we could check inside the call when implementing as a function?
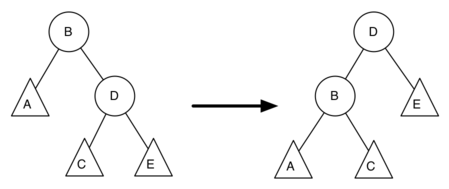
Show the function calls needed to build the following binary tree.
Given the following tree, perform the appropriate rotations to bring it back into balance.
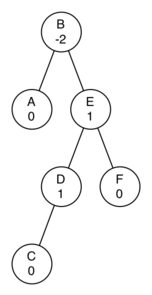
Using the following as a starting point, derive the equation that gives the updated balance factor for node D.