10.4. Market Basket Analysis¶
For retailers to increase sales and make as much profit, they need to know their customers and understand their needs and behaviors. To do this, retailers use a technique called market basket analysis. Market basket analysis consists of analyzing large data sets that include purchase history, revealing product groupings, and products that are likely to be purchased together.
The key question in the market basket analysis is what products are most frequently purchased together.
To answer this question, we will want to build a table where each row is a product, each column is a product, and the cell where two products intersect is the count of the number of times they ended up in the same shopping cart.
mb = pd.DataFrame({
'doritos': {
'oreos': 2,
'snickers':6
},
'oreos': {
'doritos': 2,
'snickers': 3
},
'snickers': {
'doritos': 6,
'oreos':3
},
})
mb
| doritos | oreos | snickers | |
|---|---|---|---|
| doritos | NaN | 2.0 | 6.0 |
| oreos | 2.0 | NaN | 3.0 |
| snickers | 6.0 | 3.0 | NaN |
Looking at the table, it is clear that Doritos and Snickers are most often purchased together because the total is 6. The next most common pair is Snickers and Oreos, that just beat out Doritos and Oreos.
Looking at the table makes answering this question fairly straightforward. We know what products have ended up in the same cart for thousands of carts.
The challenge is that we have a table with 49,688 columns and 49,688 rows. That means we have 2,468,897,344 (that is more than 2 billion!) cells in our table. How many of those cells do you think are empty?
products = pd.read_csv('ecomm/products.csv')
products.head()
| product_id | product_name | aisle_id | department_id | |
|---|---|---|---|---|
| 0 | 1 | Chocolate Sandwich Cookies | 61 | 19 |
| 1 | 2 | All-Seasons Salt | 104 | 13 |
| 2 | 3 | Robust Golden Unsweetened Oolong Tea | 94 | 7 |
| 3 | 4 | Smart Ones Classic Favorites Mini Rigatoni Wit... | 38 | 1 |
| 4 | 5 | Green Chile Anytime Sauce | 5 | 13 |
The most common operation we are going to want to use with this table is to look up a product id to get more information about the product. So, let’s make the product_id the index of the DataFrame to make things faster.
products.set_index('product_id', inplace=True)
products.head()
| product_name | aisle_id | department_id | |
|---|---|---|---|
| product_id | |||
| 1 | Chocolate Sandwich Cookies | 61 | 19 |
| 2 | All-Seasons Salt | 104 | 13 |
| 3 | Robust Golden Unsweetened Oolong Tea | 94 | 7 |
| 4 | Smart Ones Classic Favorites Mini Rigatoni Wit... | 38 | 1 |
| 5 | Green Chile Anytime Sauce | 5 | 13 |
len(products)**2
2468897344
10.4.1. Constructing an Item-Item Matrix¶
Constructing a matrix of the kind shown above will take a bit of thought (and time!). So let’s do some design first.
It’s a very good assumption that this data is sparse, so let’s start by using a data structure that supports sparsity. A dictionary of dictionaries is the key to this. In fact, scroll back just a bit and look carefully at how our DataFrame was constructed. You will notice a dictionary like this:
{ 'doritos': { 'oreos': 2, 'snickers':6 }, 'oreos': { 'doritos': 2, 'snickers': 3, }, 'snickers': { 'doritos': 6, 'oreos': 3, }, }If you think about it, you will realzse that we are storing twice as much data as we need to since the matrix we are building is symmetric; the value at position
(i, j)will always match the value at position(j, i), because the order of the products is not important.The primary source of our data will be the
order_products__traindata. The data is sorted by the order number and the order in which products were added to the cart. We want to take each order as a group and add all pairs of items in a cart to the matrix.We can take advantage of the symmetry by ordering the products in the same cart by their product id and always using the lower number as the first index.
Let’s make a simple data file that matches our example and see how we can build a sparse version of it.
1 = doritos 2 = oreos 3 = snickers
ordernum,product
1, 1
1, 2
1, 3
2, 1
2, 3
3, 1
4, 1
4, 2
5, 1
5, 3
6, 1
6, 3
7, 1
7, 3
7, 3
8, 2
8, 3
small_o = pd.read_csv('small_orders.csv')
groups = small_o.groupby('ordernum')
groups.get_group(6)
| ordernum | product | |
|---|---|---|
| 10 | 6 | 1 |
| 11 | 6 | 3 |
The get_group function is awesome! This allows us to get a data frame
containing only the items in one particular order. Now, if we are smart and
process the items from smallest to largest, we can build our dictionary-based
matrix easily.
groups.get_group(1)['product'].sort_values()
0 1
1 2
2 3
Name: product, dtype: int64
cart = groups.get_group(1)['product'].sort_values()
cart.loc[1:]
1 2
2 3
Name: product, dtype: int64
for g in range(1,9):
cart = groups.get_group(g)['product'].sort_values()
for i in cart.index:
for j in cart.loc[i+1:]:
print(f"products {cart[i]} and {j} in cart")
print("--")
products 1 and 2 in cart
products 1 and 3 in cart
products 2 and 3 in cart
--
products 1 and 3 in cart
--
--
products 1 and 3 in cart
--
products 1 and 3 in cart
--
products 1 and 3 in cart
--
products 1 and 2 in cart
products 1 and 3 in cart
products 2 and 3 in cart
--
products 2 and 3 in cart
--
mat = {}
for g in range(1,9):
cart = groups.get_group(g)['product'].sort_values().tolist()
for i in range(len(cart)):
print(mat)
if cart[i] not in mat:
mat[cart[i]] = {}
for j in cart[(i+1):]:
print(cart[i], j)
mat[cart[i]][j] = mat[cart[i]].get(j, 0) + 1
print("--")
pd.DataFrame(mat)
{}
1 2
1 3
{1: {2: 1, 3: 1}}
2 3
{1: {2: 1, 3: 1}, 2: {3: 1}}
--
{1: {2: 1, 3: 1}, 2: {3: 1}, 3: {}}
1 3
{1: {2: 1, 3: 2}, 2: {3: 1}, 3: {}}
--
{1: {2: 1, 3: 2}, 2: {3: 1}, 3: {}}
--
{1: {2: 1, 3: 2}, 2: {3: 1}, 3: {}}
1 3
{1: {2: 1, 3: 3}, 2: {3: 1}, 3: {}}
--
{1: {2: 1, 3: 3}, 2: {3: 1}, 3: {}}
1 3
{1: {2: 1, 3: 4}, 2: {3: 1}, 3: {}}
--
{1: {2: 1, 3: 4}, 2: {3: 1}, 3: {}}
1 3
{1: {2: 1, 3: 5}, 2: {3: 1}, 3: {}}
--
{1: {2: 1, 3: 5}, 2: {3: 1}, 3: {}}
1 2
1 3
{1: {2: 2, 3: 6}, 2: {3: 1}, 3: {}}
2 3
{1: {2: 2, 3: 6}, 2: {3: 2}, 3: {}}
--
{1: {2: 2, 3: 6}, 2: {3: 2}, 3: {}}
2 3
{1: {2: 2, 3: 6}, 2: {3: 3}, 3: {}}
--
| 1 | 2 | 3 | |
|---|---|---|---|
| 2 | 2 | NaN | NaN |
| 3 | 6 | 3.0 | NaN |
mat
{1: {2: 2, 3: 6}, 2: {3: 3}, 3: {}}
Now we have a “co-occurrence matrix”; given one product, we can tell how often that product is in the same shopping cart as many others. The matrix we have built turns out to be a “lower triangular matrix” because we are only storing the lower left. The upper right is symmetric so we can save half the storage!
Important: Saving storage often comes with an additional cost in complexity. In this case, because we are building a “lower triangular” matrix, we have to be careful if we want to get all of the products that are purchased together. We cannot just look at the column corresponding to the product and we cannot just look at the row corresponding to the product. If we wanted to know everything purchased with product 2, we have to look at the row for 2 as well as the column for 2. The row for 2 tells us that 2 was purchased with 1 (2 times) and the column for 2 tells us that 2 was purchased with 3 (3 times). If we kept both triangles we could look at either the row or the column.
Let’s build the item-item matrix for the instacart data and see what we can learn!
The first thing we’ll need is a list of unique order ids. In the toy example above, we were able to just use a range of numbers, because we knew that the numbers started at 1 and went sequentially.
order_products = pd.read_csv("ecomm/order_products__prior.csv")
order_products.head()
| order_id | product_id | add_to_cart_order | reordered | |
|---|---|---|---|---|
| 0 | 2 | 33120 | 1 | 1 |
| 1 | 2 | 28985 | 2 | 1 |
| 2 | 2 | 9327 | 3 | 0 |
| 3 | 2 | 45918 | 4 | 1 |
| 4 | 2 | 30035 | 5 | 0 |
import ipywidgets
def log_progress(sequence, every=None, size=None, name='Items'):
from ipywidgets import IntProgress, HTML, VBox
from IPython.display import display
is_iterator = False
if size is None:
try:
size = len(sequence)
except TypeError:
is_iterator = True
else:
if every is None:
if size <= 200:
every = 1
else:
every = int(size / 200) # every 0.5%
else:
assert every is not None, 'sequence is iterator, set every'
if is_iterator:
progress = IntProgress(min=0, max=1, value=1)
progress.bar_style = 'info'
else:
progress = IntProgress(min=0, max=size, value=0)
label = HTML()
box = VBox(children=[label, progress])
display(box)
index = 0
try:
for index, record in enumerate(sequence, 1):
if index == 1 or index % every == 0:
if is_iterator:
label.value = '{name}: {index} / ?'.format(
name=name,
index=index)
else:
progress.value = index
label.value = u'{name}: {index} / {size}'.format(
name=name,
index=index,
size=size)
yield record
except:
progress.bar_style = 'danger'
raise
else:
progress.bar_style = 'success'
progress.value = index
label.value = "{name}: {index}".format(
name=name,
index=str(index or '?'))
%%time
groups = order_products.groupby('order_id')
unique_order_ids = order_products.order_id.unique()
mat = {}
for g in log_progress(unique_order_ids, size=len(unique_order_ids)):
cart = groups.get_group(g)['product_id'].sort_values().tolist()
for i in range(len(cart)):
if cart[i] not in mat:
mat[cart[i]] = {}
for j in cart[i+1:]:
mat[cart[i]][j] = mat[cart[i]].get(j,0) + 1
VBox(children=(HTML(value=''), IntProgress(value=0, max=3214874)))
CPU times: user 39min 39s, sys: 21.5 s, total: 40min
Wall time: 40min 15s
A bit of analysis revealed that there are a HUGE number of entries in the matrix that are a count of 1. These 1-time “co-purchases” don’t give us much useful information for recommending products, so let’s save some memory and remove them.
You can’t remove things from a dictionary while you are iterating over a dictionary. So we will need to make a list of keys to remove in one pass and then delete them later.
delkeys = []
for i in mat.keys():
for k,v in mat[i].items():
if v == 1:
delkeys.append((i,k))
len(delkeys)
21944168
21.9 million entries in our matrix are 1s.
for i,j in delkeys:
del mat[i][j]
%%time
smat = pd.SparseDataFrame(mat)
smat.head()
CPU times: user 10min 55s, sys: 33.8 s, total: 11min 29s
Wall time: 11min 41s
We can check on the density of our sparse data structure by looking at its density attribute.
smat.density
0.008275774966857377
And we see that it is only 0.8% full!
We can use idxmax to give us a series that for each column tells us the row
with the maximum value for that column.
maxcols = smat.idxmax()
maxcols = maxcols.dropna()
%%time
maxcc = 0
maxrow = None
maxcol = None
for col, row in maxcols.astype(int).iteritems():
if smat.loc[row, col] > maxcc:
maxrow = row
maxcol = col
maxcc = smat.loc[row,col]
CPU times: user 1.46 s, sys: 1.86 s, total: 3.32 s
Wall time: 5.95 s
maxcc
62341.0
maxrow
47209
maxcol
13176
10.4.2. Testing The Item-Item Matrix¶
Let’s test the matrix by doing some exploring. What are the two products most commonly purchased together?
print(f"product {maxrow} was purchased with {maxcol} {maxcc} times")
product 47209 was purchased with 13176 62341.0 times
Because we were smart before and made the product_id the index of the products table, we can use this nice lookup syntax to get the product name!
products.loc[maxrow, 'product_name']
'Organic Hass Avocado'
products.loc[maxcol, 'product_name']
'Bag of Organic Bananas'
def get_product_by_id(df, idx):
return df.loc[idx].product_name
Now, let’s see what our real data has to say about the products that are bought with Doritos.
products[products.product_name.str.contains('Dorito')]
| product_name | aisle_id | department_id | |
|---|---|---|---|
| product_id | |||
| 2144 | Doritos | 107 | 19 |
| 12540 | Doritos Nacho Cheese Sandwich Crackers | 78 | 19 |
| 42541 | Cheetos Flamin' Hot & Doritos Dinamita Chile L... | 107 | 19 |
def get_product_count(sp_mat, ix1, ix2):
if ix1 > ix2:
return sp_mat.loc[ix1, ix2]
else:
return sp_mat.loc[ix2, ix1]
get_product_count(smat, 47209, 13176)
62341.0
def get_all_cocart(sp_mat, pid):
"""
Return a Pandas series where the index is the product id of products that
were in the same shopping cart. The value indicates the count of those
times. Remove the NA's.
"""
return pd.concat((sp_mat[pid], sp_mat.loc[pid])).dropna()
get_all_cocart(smat, 2144).nlargest(10)
24852 68.0
16797 41.0
19734 34.0
16696 25.0
23909 25.0
45064 24.0
28199 23.0
10673 21.0
17122 21.0
13249 17.0
Name: 2144, dtype: float64
for idx, val in get_all_cocart(smat, 2144).nlargest(10).iteritems():
print(get_product_by_id(products,idx), val)
Banana 68.0
Strawberries 41.0
Classic Mix Variety 34.0
Coke Classic 25.0
2% Reduced Fat Milk 25.0
Honey Wheat Bread 24.0
Clementines, Bag 23.0
Original Nooks & Crannies English Muffins 21.0
Honeycrisp Apples 21.0
Skim Milk 17.0
get_product_by_id(products, 2144)
'Doritos'
def product_search(df, name):
prods = df.product_name.str.lower()
return df[prods.str.contains(name)].product_name
product_search(products, 'diapers')
product_id
15 Overnight Diapers Size 6
682 Cruisers Diapers Jumbo Pack - Size 5
765 Swaddlers Diapers Jumbo Pack Size Newborn
879 Baby Dry Diapers Size 4
1304 Little Movers Comfort Fit Size 3 Diapers
1716 Baby Dry Pampers Baby Dry Diapers Size 5 78 Co...
3087 Baby Dry Pampers Baby Dry Diapers Size 2
3277 Overnight Diapers Sleepy Sheep Size 4
4630 Baby Dry Pampers Baby Dry Newborn Diapers Size...
5444 Little Snugglers Jumbo Pack Size 2 Disney Diap...
5657 Baby Dry Diapers Size 5
5897 Baby Dry Diapers Size 3
6401 Tender Care Diapers Jumbo Pack - Size 4
6986 Diapers, Overnight, Free & Clear, Size 6 (35+ ...
7487 Swaddlers Diapers Size 1
7489 Swaddlers Size 4 Giant Pack Diapers
8102 Naty Diapers Size 1, 8-14 lbs
9121 Diapers Cruisers Size 4 Super Pack
9356 Swaddlers Size 2 Diapers
9482 Diapers Size 1
9927 Size 4 Snug & Dry Diapers
10011 Baby Diapers Size 2
10420 Honest Diapers Size 4
11660 Tribal Pastel Size 3 Diapers
11745 Swaddlers Sensitive Diapers Jumbo Pack Size Ne...
11922 Pants Pampers Easy Ups Training Pants Boys Siz...
12340 Free & Clear Size 4 Baby Diapers
13377 Swaddlers Diapers Jumbo Pack Size
13801 Free & Clear Overnight Diapers Size 5
14009 Snug & Dry Diapers Step 1 Jumbo
...
35954 Little Movers Diapers, Giant Pack - Size 5
36200 Baby Dry Diapers Size 6 Diapers
36453 Size 3 M Skulls Diapers
36831 Cruisers Diapers Giant Pack, Size 6
37172 Size 4 Diapers
37872 Free & Clear Size 4 22-37 Lbs Disposable Diapers
37949 Diapers Swaddlers Size 2 (12-18 lb)
38365 Size 5 Cruisers Diapers Super Pack
38899 Little Movers Size 3 Diapers
40110 Giraffes Diapers Size 4 L
40343 Baby Dry Diapers Giant Pack - Size 6
40355 Baby Dry Size 4 Disposable Diapers
40537 Free & Clear Stage 1 8-14 Lbs. Baby Diapers
40916 Size 2 Diapers
41393 Baby Dry Size 4 Diapers
41475 Baby Dry Diapers Jumbo Pack Size 4
41595 Snug & Dry Size 2 Diapers
41705 Honest Diapers Size 3
42923 Baby Free & Clear Size 3 16-28 Lbs Diapers
43217 Honest Diapers Eco-Friendly & Premium Diapers ...
43481 Cruisers Diapers Jumbo Pack Size 3
43989 Cruisers Diapers - Size 6
44950 Swaddlers Diapers Super Pack, Size 3
45786 Little Movers Diapers Giant Pack - Size 3
46583 Tribal Pastel Size 4/L Diapers
46599 Ultra Leakguards Value Pack Diapers Size 3 (16...
46608 Free & Clear Newborn Up To 10 lbs Baby Diapers
47578 Diapers
47632 Honest Diapers
48263 Honest Diapers Size 5
Name: product_name, Length: 93, dtype: object
# snickers - 14261
for idx, val in get_all_cocart(smat, 682).nlargest(10).iteritems():
print(get_product_by_id(products,idx), val)
Strawberries 13.0
Banana 13.0
Zero Rise Orange 7.0
Organic Fuji Apple 7.0
Baby Fresh Pampers Baby Wipes Baby Fresh 1X 64 count Baby Wipes 6.0
Black Beans 6.0
Honey Nut Cheerios 6.0
Baby Wipes Sensitive 6.0
Select-A-Size Paper Towels, White, 2 Huge Rolls = 5 Regular Rolls Towels/Napkins 5.0
Peach Yoghurt 5.0
10.4.3. Cleaning Up and Saving¶
Since building the item-item matrix takes some time, we should save it in a format that is convenient for us to reload so we don’t need to remake it every time.
We can probably reduce the size of our sparse matrix by eliminating all of the cells with a count of 1. That doesn’t really tell us anything that we would want to use in making a recommendations. We can also eliminate our original dictionary.
smat.to_pickle('item_item.pkl')
10.4.4. Understanding the Item-Item Matrix¶
This kind of shopping cart analysis is useful in many areas. Whether it’s news articles, stocks, search terms, or products, this kind of recommender is widely used in industry.
Create a histogram that shows the distribution of the shopping cart co-occurrence counts.
How many items in this item-item matrix contain a count of 1? That is probably not good information and you could save a lot more memory by deleting all of the items with a count of 1 from smat.
Can you make a visualization of this item-item matrix?
forhist = pd.DataFrame({'allvals': smat.values.flatten()})
forhist = forhist.dropna()
alt.Chart(forhist).mark_bar().encode(
x=alt.X('allvals', bin=True),y='count()')
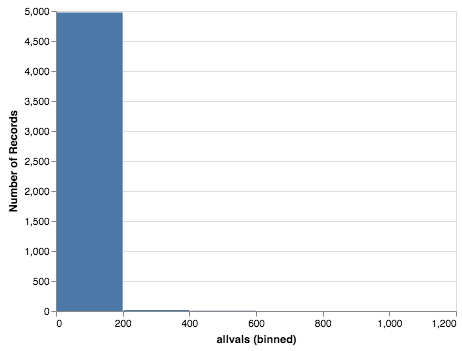
10.4.5. Experimenting with Item-Item Recommendations¶
The histogram above shows that the vast majority of the items are in the 0-200 co-occurrence range. But the items purchased together outside that big bar are interesting. Write a function to print out the item pairs that have been in the same shopping cart more than 200 times.
Redo the histogram so that it focuses in on the products that have between 0 and 200 co-occurrences.
Write a function called
top_nthat takes a product name to search for, allows the user to select the best match, and then returns the topnrecommendations for products that have been purchased with the selected item.Write a function that takes a product id as its parameter and then recommends the top 10 products to go with the given product but from the same department or same aisle.
One of the problems with a recommender like this one is that it tends to recommend a lot of popular items. We might call this the banana problem in this dataset! Can you devise a strategy to recommend things that are not just popular?
Design an experiment in which you can train an item-item model like we have done above and then test it. Perhaps in the training set you withhold that last item added to the shopping cart to see how frequently you can predict the last item based on the first items.
Challenge: The original collaborative filtering recommender system was not item-item like this was. It was user-user where the recommendations came from finding a group of users similar to the subject user based on their ratings or purchase behavior. The system would then recommend items to the subject user based on items that their similar users had purchased but the subject had not. Can you write such a recommender and devise an experiment to compare it to the item-item recommender?
Lesson Feedback
-
During this lesson I was primarily in my...
- 1. Comfort Zone
- 2. Learning Zone
- 3. Panic Zone
-
Completing this lesson took...
- 1. Very little time
- 2. A reasonable amount of time
- 3. More time than is reasonable
-
Based on my own interests and needs, the things taught in this lesson...
- 1. Don't seem worth learning
- 2. May be worth learning
- 3. Are definitely worth learning
-
For me to master the things taught in this lesson feels...
- 1. Definitely within reach
- 2. Within reach if I try my hardest
- 3. Out of reach no matter how hard I try