11.1.5. Tracing Recursive Methods¶
In Java, the call stack keeps track of the methods that you have called since the main method executes. A stack is a way of organizing data that adds and removes items only from the top of the stack. An example is a stack of cups. You can grap a cup from the top of the stack or add more cups at the top of the stack.

Figure 2: Stacks of cups¶
When you are executing one method (method a) and it calls another method (method b) the method call is placed on the call stack along with information about where it was called from, which tells the run-time where to return to when the current method finishes executing. When method b finishes executing the run-time pops the method b off of the call stack and returns execution to the next line to be executed in method a.
Consider the following class definition.
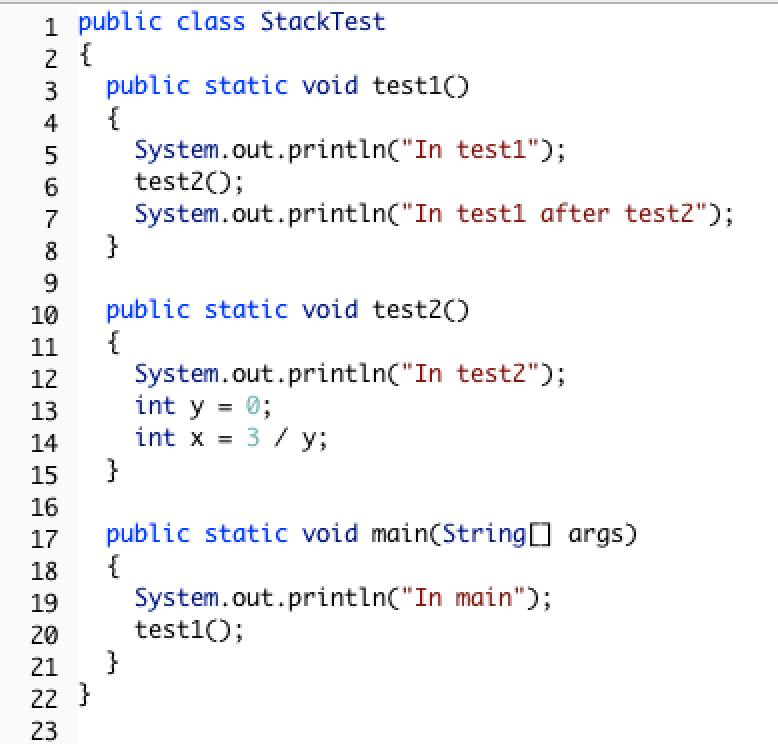
Figure 3: Code with a divide by zero in a method.¶
The code above will cause a run-time error of division by zero when it runs. The main method calls the method test1 (at line 20) which calls the method test2 (at line 6) which has the divide by zero error (line 14). This can be seen in the call stack shown below which shows the call stack from the top (most recent method) to the bottom (first method call).
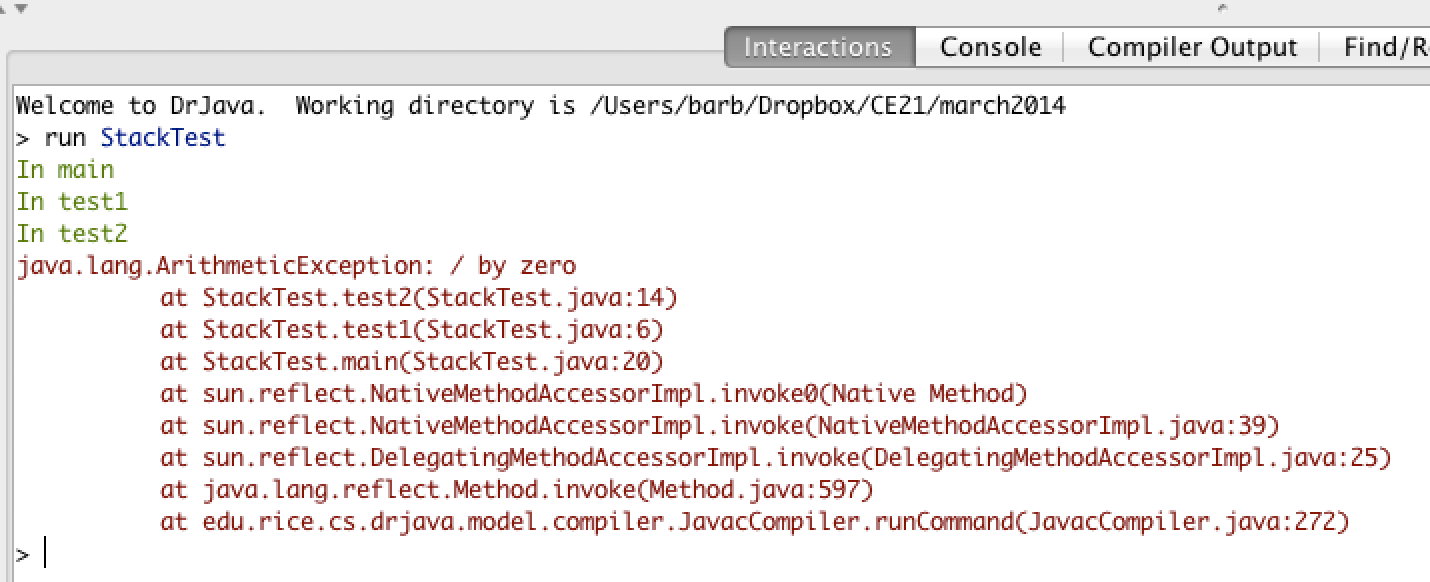
Figure 4: A call stack in DrJava with a run-time error¶
When a method calls itself the new method call gets added to the top of the call stack. Execution of the current method pauses while the recursive call is being processed. Each recursive call on the stack has its own set of local variables, including the parameter variables. The parameter values progressively change in each recursive call until we reach the base case which stops the recursion.
Let’s trace the execution of the factorial method defined below.
public static int factorial(int n)
{
if (n == 0)
return 1;
else
return n * factorial(n-1);
}
What happens when we call factorial(0)? It will return 1 (line 4) since n is equal to 0. How about factorial(1)? It will return 1 * factorial(0). We already know that factorial(0) returns 1, but the computer won’t remember that. It will execute factorial(0) and return the result (1). So factorial(1) returns 1 * 1 which is 1.
How can you show what is happening in a recursive call? Here is one way to do it. The lines below show the call stack upside down (with the bottom of the stack, or the beginning at the top and the most recent call at the bottom) for a call to factorial(5). This is a handy way to trace a recursive method on the exam and you will do much better on recursive problems if you practice doing it this way.
factorial(5) returns 5 * factorial(4)
factorial(4) returns 4 * factorial(3)
factorial(3) returns 3 * factorial(2)
factorial(2) returns 2 * factorial(1)
factorial(1) returns 1 * factorial(0)
factorial(0) returns 1
Once factorial(0) executes and returns 1 that value can be substituted back into the previous method call, starting at the top of the stack (shown at the bottom here) and working our way back to the bottom of the stack (shown at the top here).
factorial(5) returns 5 * factorial(4) = 5 * 24 = 120
factorial(4) returns 4 * factorial(3) = 4 * 6 = 24
factorial(3) returns 3 * factorial(2) = 2 so 3 * 2 = 6
factorial(2) returns 2 * factorial(1) = 1 so 2 * 1 = 2
factorial(1) returns 1 * factorial(0) = 1 so 1 * 1 = 1
factorial(0) returns 1
So factorial(5) returns 120.
You can step through this code using the Java Visualizer by clicking on this link: factorial.
Another way to see the call stack in action is to download and use the Jeloit software (see http://cs.joensuu.fi/jeliot/).
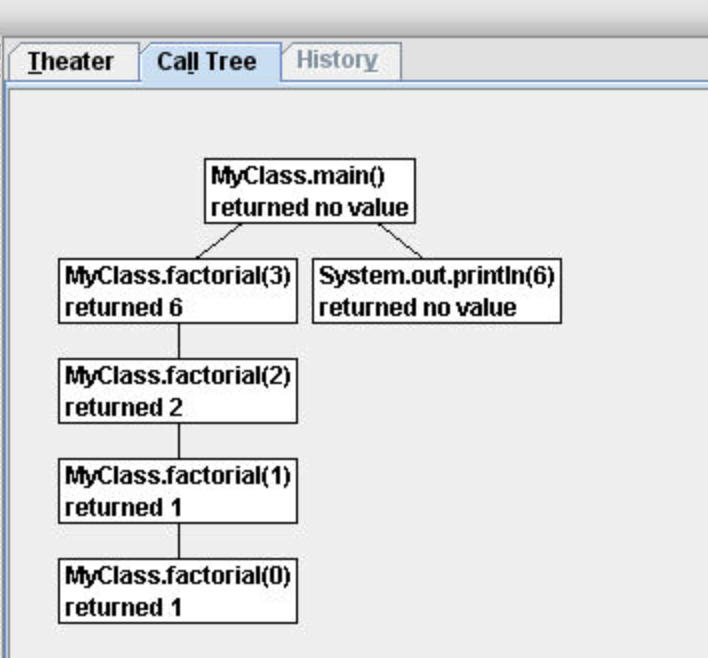
Figure 5: A call tree in Jeliot¶
- 1
- This would be correct if it was factorial(0), but don't forget the recursive calls.
- 120
- This would be correct if it was factorial(5), but this is factorial(6).
- 720
- If you remember that factorial(5) was 120 then this is just 6 * 120 = 720.
- 30
- It doesn't return 6 * 5 it returns 6 * factorial(5).
11-1-9: Given the method defined below what does the following return: factorial(6)?
1public static int factorial(int n) 2{ 3 if (n == 0) 4 return 1; 5 else 6 return n * factorial(n-1); 7}
- 10
- This would be correct if it addition instead of multiplication.
- 32
- This method calculates 2 raised to the nth power.
- 16
- Check that you didn't miss one of the recursive calls.
- 64
- This would be true if the call was mystery(6).
11-1-10: Given the method defined below what does the following return: mystery(5)?
1public static int mystery(int n) 2{ 3 if (n == 0) 4 return 1; 5 else 6 return 2 * mystery (n - 1); 7}
You can step through the code above using the Java Visualizer by clicking on the following link: Ex-11-3-2.
- 12
- This would be correct if it added instead of multiplied.
- 81
- This calculates a to nth power.
- 64
- This would be correct if it was 4 to the 3rd instead of 3 to the 4th power.
- 27
- This would be correct if returned 1 instead of a in the base case.
- 243
- This would be correct if it was 3 to the 5th.
11-1-11: Given the method defined below what does the following print: mystery(4,3)?
1public static int mystery(int n, int a) 2{ 3 if (n == 1) return a; 4 return a * mystery(n-1,a); 5}
You can step through the code above using the Java Visualizer by clicking on the following link: Ex-11-3-3.
Let’s trace the execution of the bunny ears method defined below.
1public static int bunnyEars(int bunnies)
2{
3 if (bunnies == 0) return 0;
4 else if (bunnies == 1) return 2;
5 else return 2 + bunnyEars(bunnies - 1);
6}
What happens when we call bunnyEars(0)? It will return 0 since n is equal to 0 (line 3). How about bunnyEars(1)? It will return 2 since n is equal to 1 (line 4). What about bunnyEars(5)?
1bunnyEars(5) returns 2 + bunnyEars(4)
2bunnyEars(4) returns 2 + bunnyEars(3)
3bunnyEars(3) returns 2 + bunnyEars(2)
4bunnyEars(2) returns 2 + bunnyEars(1)
5bunnyEars(1) returns 2
This approach shows the call stack from bottom to top. Once bunnyEars(1) executes and returns 2 that value can be substituted back into the previous method call, starting at the top and working our way back toward the bottom (or beginning) of the call stack.
1bunnyEars(5) returns 2 + bunnyEars(4) = 2 + 8 = 10
2bunnyEars(4) returns 2 + bunnyEars(3) = 2 + 6 = 8
3bunnyEars(3) returns 2 + bunnyEars(2) = 2 + 4 = 6
4bunnyEars(2) returns 2 + bunnyEars(1) = 2 + 2 = 4
5bunnyEars(1) returns 2
So bunnyEars(5) returns 10. You can step through this code using the Java Visualizer by clicking on this link: bunnyEars.
- 12344321
- Remember that 1234 % 10 returns the rightmost digit.
- 1234
- There are two calls that print something in this method.
- 4321
- There are two calls that print something in this method.
- 43211234
- This method prints the right most digit and then removes the rightmost digit for the recursive call. It prints both before and after the recursive call.
- 32144123
- Since 1234 % 10 returns the rightmost digit, the first thing printed is 4.
11-1-12: Given the method defined below what does the following print: mystery(1234)?
1public static void mystery (int x) { 2 System.out.print(x % 10); 3 4 if ((x / 10) != 0) { 5 mystery(x / 10); 6 } 7 System.out.print(x % 10); 8}
You can step through the code above using the Java Visualizer by clicking on the following link: Ex-11-3-4.
- 7
- This would be correct if was counting the number of characters in the string, but that isn't what it is doing.
- 2
- This method seems to be counting the number of y's in the string, but fails to check if a single character is a y.
- 1
- Don't forget that there are recursive calls too.
- 3
- This would be correct if the base case returned 1 if the single character was a y.
- 0
- Don't forget about the recursive calls.
11-1-13: Given the method defined below what does the following return: mystery(“xyzxyxy”)? Note that this recursive method traverses a String.
1public static int mystery(String str) 2{ 3 if (str.length() == 1) return 0; 4 else 5 { 6 if (str.substring(0,1).equals("y")) return 1 + 7 mystery(str.substring(1)); 8 else return mystery(str.substring(1)); 9 } 10}
You can step through the code above using the Java Visualizer by clicking on the following link: Ex-11-3-5
Continue to the next page for the Recursion lesson challenge and summary.

