7.5. Randomness¶
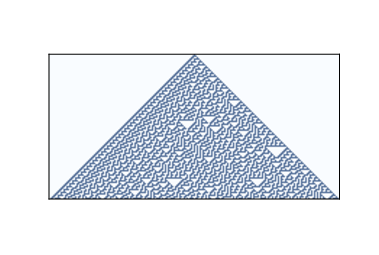
Figure 7.3: Rule 30 after 100 time steps.¶
Class 3 contains CAs that generate randomness. Rule 30 is an example; Figure 7.3 shows what it looks like after 100 time steps.
Along the left side there is an apparent pattern, and on the right side there are triangles in various sizes, but the center seems quite random. In fact, if you take the center column and treat it as a sequence of bits, it is hard to distinguish from a truly random sequence. It passes many of the statistical tests people use to test whether a sequence of bits is random.
Programs that produce random-seeming numbers are called pseudo-random number generators (PRNGs). They are not considered truly random because:
Many of them produce sequences with regularities that can be detected statistically. For example, the original implementation of
randin the C library used a linear congruential generator that yielded sequences with easily detectable serial correlations.Any PRNG that uses a finite amount of state (that is, storage) will eventually repeat itself. One of the characteristics of a generator is the period of this repetition.
The underlying process is fundamentally deterministic, unlike some physical processes, like radioactive decay and thermal noise, that are considered to be fundamentally random.
Modern PRNGs produce sequences that are statistically indistinguishable from random, and they can be implemented with periods so long that the universe will collapse before they repeat. The existence of these generators raises the question of whether there is any real difference between a good quality pseudo-random sequence and a sequence generated by a “truly” random process. In A New Kind of Science, Wolfram argues that there is not (pages 315–326).
- One of the main characteristics of pseudo-random generators are that they have a regular frequency.
- Incorrect, they have a regular sequence not a regualr frequency.
- The underlying process is fundamentally deterministic.
- Correct, this means that produce sequences with regularities that can be detected statistically.
- Any PRNG that uses a finite amount of state will eventually repeat itself.
- Correct, any PRNG that uses a finite amount of storage will eventually repeat itself.
- Many of them produce sequences with regularities that can be detected X statistically.
- Correct.
- It has passed scientific random tests
- Incorrect. Modern PRNGs produce sequences that are statistically indistinguishable from random, and they can be implemented with periods so long that the universe will collapse before they repeat. The existence of these generators raises the question of whether there is any real difference between a good quality pseudo-random sequence and a sequence generated by a “truly” random process.
Q-1: Why are pseudo-random number generators (PRNGs) not considered truly random? Select all that apply.