5.2. Procedures and Functions¶
We have seen string functions like lower() which returns a new string with all lowercase characters. Functions return a value. The Screen() and Turtle() in the code below both create objects and return them, so they are functions. You can also have procedures which do some action, but don’t return anything. The forward(75) and left(90) below are both procedures since they do an action, but don’t return anything.
Note
Some Python books don’t make a distinction between procedures and functions and will call both of these functions. In this book we are using function only for named code that returns a value and procedure for named code that doesn’t return a value.
What letter (like A, B, C, D, etc) will the program below draw in block style when you click on the Run button?
Check Your Understanding
- function
- Does it return a value?
- procedure
- The right procedure will cause the turtle to turn right by the specified number of degrees and doesn't return any value so it is a procedure.
Is right(90) a function or procedure?
Note
In these next problems we will draw a letter similar to how you might do it without lifting your pen or pencil. See the numbers and arrows on the letters for the order that the lines are drawn.
Mixed up programs
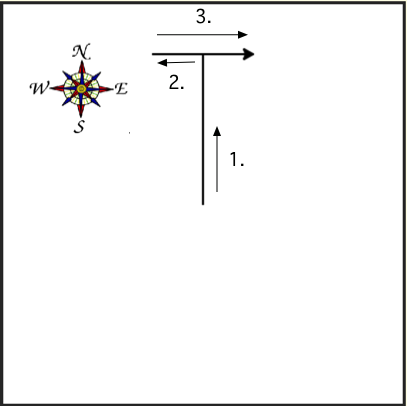
The following program uses a turtle to draw a capital T as shown below but the lines are mixed up. The program should do all necessary set-up: import the turtle module, get the space to draw on, and create the turtle. After that the turtle should draw the lines in the numbered order as shown in the picture on the left. Drag the needed blocks of statements from the left column to the right column and put them in the right order. Then click on Check Me to see if you are right. You will be told if any of the lines are in the wrong order or are the wrong blocks.
Mixed up programs
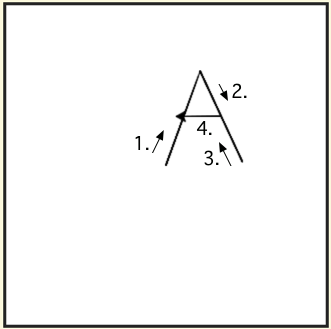
The following program uses a turtle to draw a capital A as shown below, but the lines are mixed up. The program should do all necessary set-up: import the turtle module, get the space to draw on, and create the turtle. After that the turtle should draw the lines in the numbered order as shown in the picture on the left. Drag the needed blocks of statements from the left column to the right column and put them in the right order. Then click on Check Me to see if you are right. You will be told if any of the lines are in the wrong order or are the wrong blocks.