7.10. What is this a Model of?¶
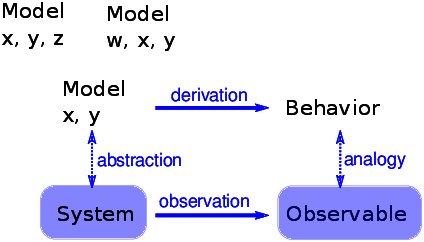
Figure 7.6: The logical structure of a simple physical model.¶
Some cellular automatons are primarily mathematical artifacts. They are interesting because they are surprising, or useful, or pretty, or because they provide tools for creating new mathematics (like the Church-Turing thesis).
But it is not clear that they are models of physical systems. And if they are, they are highly abstracted, which is to say that they are not very detailed or realistic.
For example, some species of cone snail produce a pattern on their shells that resembles the patterns generated by cellular automatons. So it is natural to suppose that a CA is a model of the mechanism that produces patterns on shells as they grow. But, at least initially, it is not clear how the elements of the model (so-called cells, communication between neighbors, rules) correspond to the elements of a growing snail (real cells, chemical signals, protein interaction networks).
For conventional physical models, being realistic is a virtue. If the elements of a model correspond to the elements of a physical system, there is an obvious analogy between the model and the system. In general, we expect a model that is more realistic to make better predictions and to provide more believable explanations.
Of course, this is only true up to a point. Models that are more detailed are harder to work with, and usually less amenable to analysis. At some point, a model becomes so complex that it is easier to experiment with the system.
At the other extreme, simple models can be compelling exactly because they are simple.
Simple models offer a different kind of explanation than detailed models. With a detailed model, the argument goes something like this: “We are interested in physical system \(S\), so we construct a detailed model, \(M\), and show by analysis and simulation that \(M\) exhibits a behavior, \(B\), that is similar (qualitatively or quantitatively) to an observation of the real system, \(O\). So why does \(O\) happen? Because \(S\) is similar to \(M\), and \(B\) is similar to \(O\), and we can prove that \(M\) leads to \(B\).”
With simple models we can’t claim that \(S\) is similar to \(M\), because it isn’t. Instead, the argument goes like this: “There is a set of models that share a common set of features. Any model that has these features exhibits behavior \(B\). If we make an observation, \(O\), that resembles \(B\), one way to explain it is to show that the system, \(S\), has the set of features sufficient to produce \(B\).”
For this kind of argument, adding more features doesn’t help. Making the model more realistic doesn’t make the model more reliable; it only obscures the difference between the essential features that cause B and the incidental features that are particular to \(S\).
Figure 7.6 shows the logical structure of this kind of model. The features x and y are sufficient to produce the behavior. Adding more detail, like features w and z, might make the model more realistic, but that realism adds no explanatory power.